또한, 이 기댓값은 다음 상태인 s′의 상태-가치 함수가 되기 때문에 ② 수식의 기댓값을 가치 함수로 변환하면 다음과 같이 사용할 수 있습니다.
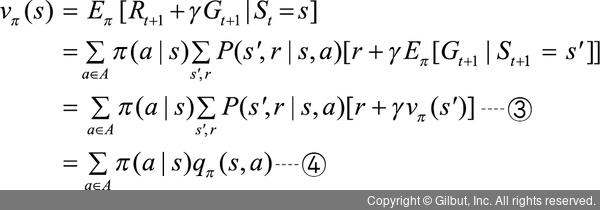
위 수식의 ③, ④를 상태-가치 함수의 벨만 방정식이라고 합니다.
이제 ④의 식에서 qπ(s,a)를 다시 풀어 써 보겠습니다.
그림 12-9와 같이 상태 s에서 행동 a를 했을 때의 행동에 대한 가치는 두 가지 요소로 구성되어 있는데, 상태 s에서 행동 a를 했을 때의 보상과 그다음 상태의 가치 함수입니다. 그런데 이 중 다음 상태-가치 함수(vπ(s'))는 t+1 시점에서의 가치 함수이므로 할인율과 현재(t) 상태 s에서 다음(t+1) 상태 s'로 전이될 확률도 적용해 주어야 합니다.
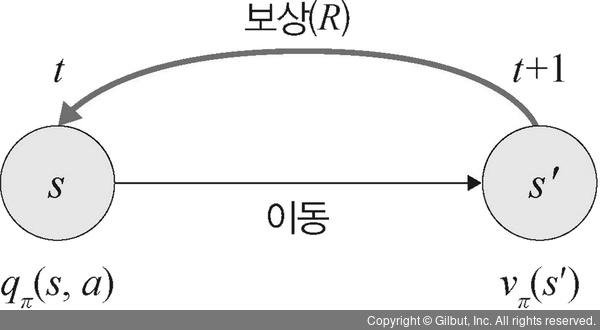
▲ 그림 12-9 상태 s에서 행동 a를 했을 때의 보상과 그다음 상태의 가치 함수