2. (μx|z, Σx|z)의 가우시안 분포에서 z를 샘플링한 후 x'를 구합니다.
x' ← x|z ~ N(μx|z, Σx|z)
3. 역전파를 이용하여 L(x(i), θ, >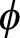
)의 값이 높아지는 방향으로 기울기를 업데이트합니다. 즉, 가능도가 증가하는 방향으로 파라미터 θ와 
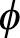를 업데이트합니다.
최종적으로 x와 유사한 x'라는 이미지가 생성됩니다.
다음은 인코더와 디코더에서 사용된 수식을 정리한 내용입니다. 변형 오토인코더의 목표는 L(x(i), θ,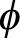 
)를 높이는 방향으로 학습합니다.
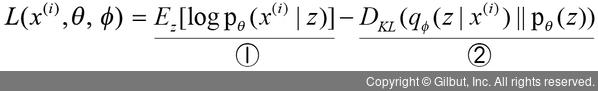
①항은 z가 주어졌을 때 x'를 표현하기 위한 확률밀도 함수로 디코더 네트워크를 나타냅니다. 즉, 디코더 네트워크의 가능도(likelihood)가 크면 클수록 θ가 그 데이터를 잘 표현한다고 해석할 수 있습니다. 따라서 ①항이 크면 클수록 모델 가능도가 커집니다.
②항은 x에서 z를 표현하는 확률밀도 함수로 인코더 네트워크와 가우시안 분포가 얼마나 유사한지 나타냅니다. 유사한 정도가 높을수록 쿨백-라이블러 발산(Kullback–Leibler Divergence, DKL6)은 낮은 값을 나타내므로, 인코더 네트워크가 가우시안 분포를 최대한 잘 표현할 수 있도록 가능도가 최대화됩니다. 따라서 ②항이 작을수록 모델 가능도가 커집니다.
이제 변형 오토인코더를 예제로 알아보겠습니다. 변형 오토인코더 예제를 시작하기에 앞서 필요한 라이브러리를 설치합니다.
> pip install tensorflow_probability
6 두 확률 분포의 차이를 계산하는 데 사용하는 함수입니다. 딥러닝 모델을 예로 들면, 수집된 데이터 분포 P(x)와 모델이 추정한 데이터 분포 Q(x)의 차이를 구할 때 사용합니다.