① reparameterize 함수는 z 분포를 이용하여 z 벡터를 샘플링합니다. z는 가우시안 분포라고 가정했기 때문에 평균(μ)과 표준편차(σ)를 이용하여 z에 노이즈(epsilon)를 적용하여 샘플링합니다. 그리고 샘플링한 z 벡터를 디코더에 다시 통과시켜서 입력과 동일한 데이터(x')를 만들어 내는 작업을 합니다.
샘플링 작업에 노이즈를 부여해서 z 벡터를 여러 개 뽑고, p(x|z)를 거치면서 기존 입력 데이터(x)와 다른 분포를 가지는 데이터(x')가 출력됩니다.
② 손실을 구하는 함수입니다. 변분추론(variational inference)7으로 p(z|x)와 q(z) 사이의 쿨백-라이블러 발산(KLD)을 계산하고, KLD가 줄어드는 쪽으로 q(z)를 조금씩 업데이트합니다. 즉, 변형 오토인코더에서 손실 함수가 쿨백-라이블러 발산이 되며, 다음 수식을 사용합니다.
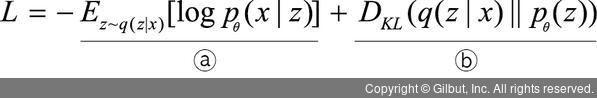
ⓐ항은 재구성 손실(reconstruction loss)에 해당하며, 인코더가 데이터 x를 받아 q에서 z를 뽑습니다. 디코더는 인코더가 만든 z를 받아 원래의 데이터 x를 복원합니다. 즉, 원 데이터에 대한 가능도를 선택합니다. ⓑ항은 인코더와 디코더 사이의 손실 함수(크로스 엔트로피)를 가리키며, 쿨백-라이블러 발산 정규화(KL divergence regularizer)에 해당됩니다. 이때 변형 오토인코더는 z의 평균이 0에 수렴하는 가우시안 분포를 가정합니다.
7 변분추론은 이상적인 확률 분포를 모르지만, 이를 추정하고자 다루기 쉬운 분포(예 가우시안 분포(gaussian distribution))를 가정하고, 이 확률 분포의 모수를 바꾸어 가며 이상적 확률 분포에 근사하게 만들어 그 확률 분포를 대신 사용하는 것입니다.