2 로그함수의 평행 이동과 대칭 이동

로그함수의 평행 이동

로그함수 y = log_ax를 평행 이동하면 지수함수와 마찬가지로 그래프 모양은 바뀌지 않으면서 위치만 바뀝니다.

즉, 그림 6-11의 ①과 같이 y = log_ax 그래프를 평행 이동한다고 가정해 봅시다.

②와 같이 x축 방향으로 p만큼 평행 이동한다면 x 대신 x - p를 대입하여 y = log_a(x - p)가 되고,

③과 같이 y축 방향으로 q만큼 평행 이동한다면 y 대신 y - q를 대입하여 y = log_ax + q가 됩니다.

또 ④와 같이 x축으로 p만큼, y축으로 q만큼 평행 이동한다면 y = log_a(x - p) + q가 됩니다.

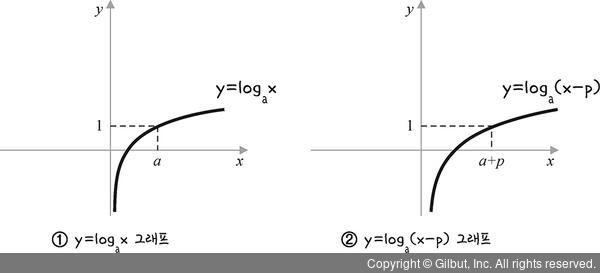
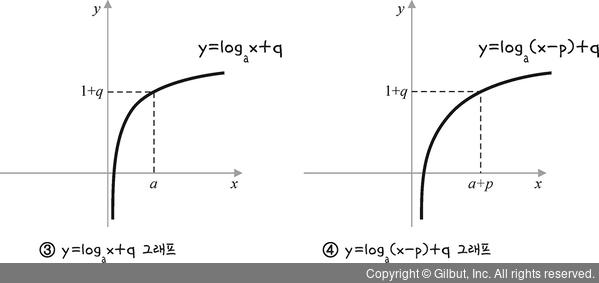
그림 6-11 | 로그함수의 평행 이동

a > 0일 때를 알아보았지만, 0 < a < 1일 때 그래프도 원리는 동일합니다.