계산한 기하평균은 한 변의 평균 길이다. 이 한 변의 길이를 가진 정사각형의 면적을 구하면 다음과 같다.

2.4494897432² = 6

즉, 기하평균은 가로와 세로의 평균 길이가 된다. 그러므로 기하평균은 곱셈의 평균인 셈이다.

기하평균은 물가상승률, 매출증가율, 인구성장률, 투자이율 등 성장률의 평균을 산출할 때 사용한다. 기하평균의 대표적인 예가 CAGR(Compound Average Growth Rate)이다. CAGR은 국가의 GDP나 기업 매출액의 성장률을 나타내는 수치다.

앞에서 산술평균과 기하평균의 개념을 다뤘는데, 이번에는 기하평균이 산술평균보다 더 유용한 경우를 살펴보자.

대부분의 수익률은 자산의 변동분을 비율로 표시한다. -10%이면 원래 자산에서 1/10이 사라진 것이고, +25%이면 원래 자산의 1/4만큼 늘어난 것이다.

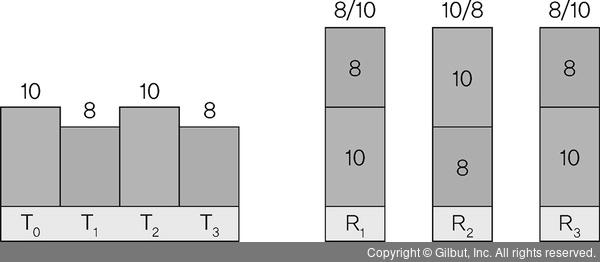
▲ 그림 1-23 T₁은 T₀ 시점과 비교한다. T는 시점, R은 해당 시점의 수익률이다