1.5.7 공분산과 상관계수

두 변수의 상관관계를 나타내는 척도로 공분산과 상관계수가 있다. 공분산 수식(표본의 공분산)은 다음과 같다.

여기서 x와 y는 각각의 변수를 의미하고 μ는 변수의 평균이다. 그리고 n은 데이터의 개수를 의미한다.

수식을 분석하면, 분모는 데이터의 개수로 나눈 것이다. 그리고 분자에 해당하는 부분 Σ(x - μ_x)(y - μ_y)를 보면 가로와 세로를 곱한 것(사각형의 면적)을 합쳐놓은 듯한 모습이다. 합계를 개수(n - 1)로 나눴다는 점에서 위의 공분산 수식은 평균의 일종임을 알 수 있다.

종합하면, 다음 그림과 같이 평균 μ를 영점으로 하는 1, 2, 3, 4로 번호를 매겨둔 네 사각형의 평균 면적이다.

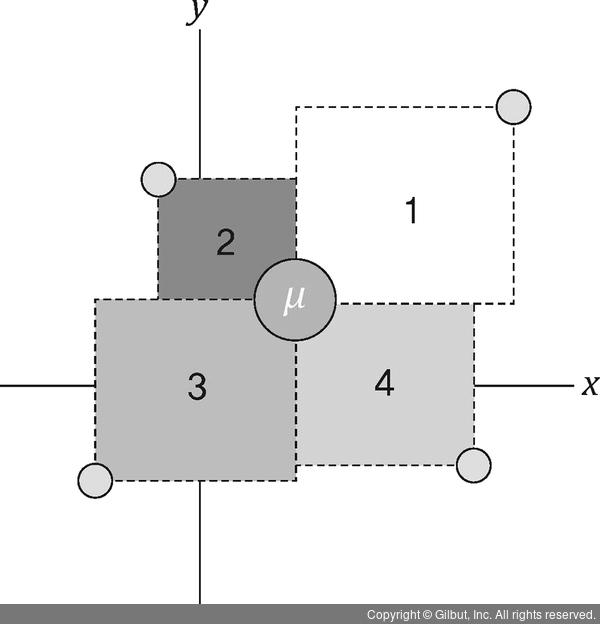
▲ 그림 1-36 공분산은 평균을 중심으로 모인 네 사각형의 평균 면적으로 생각할 수 있다