상관계수 식은 분수 형태, 즉 공분산과 두 변수의 표준편차곱 간의 비율이다. 두 변수의 표준편차를 곱하는 것이므로 가로와 세로의 길이가 표준편차인 사각형 위에 공분산을 올려둔 것으로 이해할 수 있다.

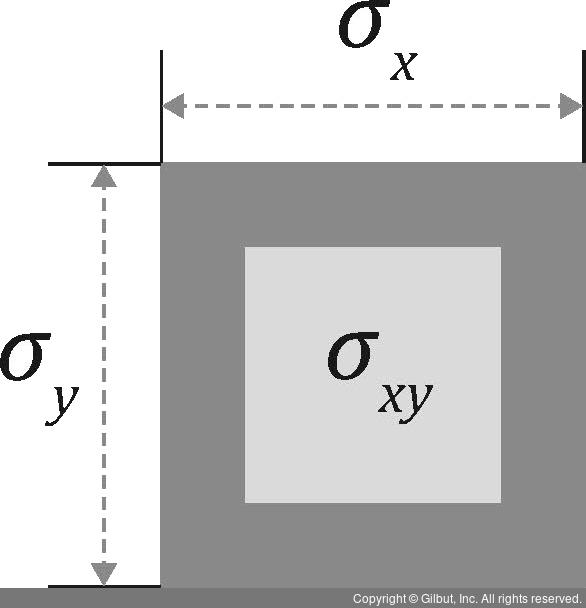
▲ 그림 1-37 상관계수는 공분산과 두 변수의 표준편차곱 간의 비율이다

상관계수는 두 변수 간의 관계를 의미한다. 그러나 두 변수 간의 연관된 정도를 나타낼 뿐 인과(원인과 결과)관계를 설명하는 것은 아니다. 두 변수 간의 인과관계는 회귀분석을 통해 확인할 수 있다. 보편적으로 많이 사용하는 상관계수는 피어슨 상관계수이며, X와 Y의 피어슨 상관계수 수식은 다음과 같다.

상관계수 r 값은 -1.0 ~ +1.0 사이의 값으로 X와 Y가 완전히 동일하면 +1.0, 전혀 다르면 0.0, 반대 방향으로 완전히 동일하면 -1.0이다. r²은 X로부터 Y를 예측할 수 있는 정도를 의미하며, 이를 결정계수(coefficient of determination)라고 한다. 결정계수는 우리가 추정하는 선형 모델이 실제 데이터에 얼마나 잘 맞는지 알려주는 적합도를 나타내는 척도다.