# 3장에서 구한 일간수익률 평균과 최적화로 얻은 투자 비중을 곱해 최소분산포트폴리오의 기대수익률을 구한다
rets = np.sum( ret_daily.mean( ) * res[ 'x' ] ) * 250

# 최소분산포트폴리오의 위험을 구한다
vol = np.sqrt( res[ 'x' ].T @ covmat @ res[ 'x' ] )

# 차트에 표시하기 위해 np.array로 변환한다. p_volatility와 p_returns는 3장에서 n_ports만큼의 포트폴리오를 만들면서 저장한 수익률과 변동성이다
p_volatility = np.array( p_volatility )
p_returns = np.array( p_returns )

# 변수 n_ports만큼 색상을 무작위로 얻어 ◌로 표시되는 포트폴리오 색상을 지정한다
colors = np.random.randint( 0, n_ports, n_ports )

# 분산형 차트를 그린다. 아래 코드 대부분은 3장에서 이미 사용한 것이며, plt.scatter( vol, rets, marker="*", s=500, alpha=1.0 )만 추가했다. 실행 결과 최소분산포트폴리오의 수익률과 위험이 분산 차트로 표시된다

plt.style.use( 'seaborn' )
plt.scatter( p_volatility, p_returns, c=colors, marker='o', cmap=mpl.cm.jet )
plt.scatter( vol, rets, marker="*", s=500, alpha=1.0 )
plt.xlabel( 'Volatility(Std. Deviation)' )
plt.ylabel( 'Expected Returns' )
plt.title( 'Efficient Frontier' )
plt.show( )

결과

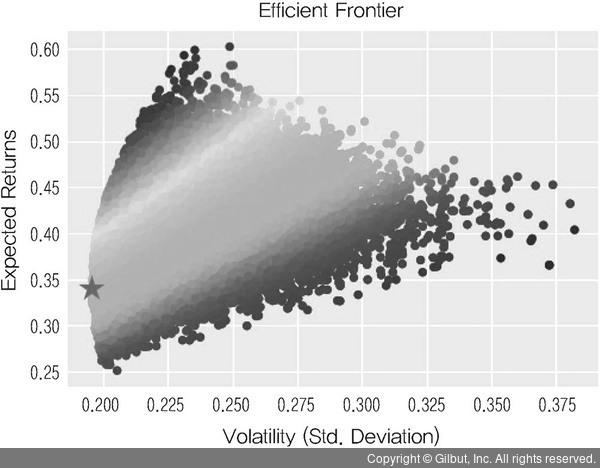
▲ 그림 4-20 최소분산포트폴리오(★)