베이즈 이론을 간단히 살펴보기 전에 먼저 확률의 덧셈정리와 곱셈정리를 알아보자.

확률의 덧셈, 즉 확률의 합사건은 P(A∪B) = P(A) + P(B) - P(A∩B)이다. 여기서 P(A∩B)는 확률의 곱셈이다. 이것은 확률의 곱사건을 의미하며 사건 A와 사건 B가 함께 일어날 확률을 말한다.

확률의 덧셈정리 P(A∪B) = P(A) + P(B) - P(A∩B)

확률의 곱셈정리 P(A∩B) = P(B|A)×P(A) = P(A|B)×P(B)

다음 그림은 베이즈 확률을 설명하기 위한 다이어그램이다.

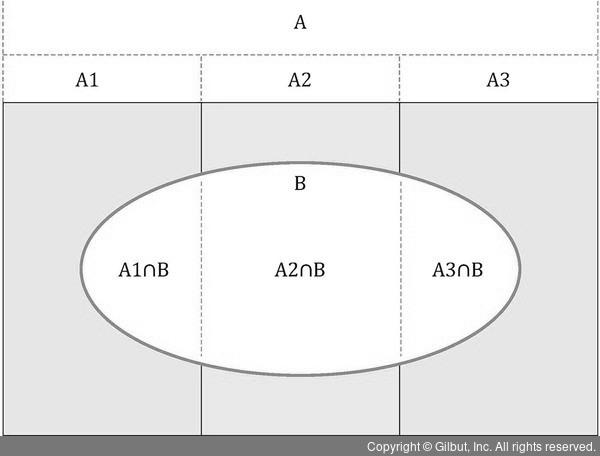
▲ 그림 5-7 베이즈 확률 다이어그램

그림에서 사건 A는 그보다 작은 소사건 A1, A2, A3로 구성된 확률공간이다. 이때 A1, A2, A3는 동시에 일어날 수 없다. 따라서 확률의 덧셈정리에 따라 셋의 확률합은 사건 A의 확률이 된다.