비용함수에서 n은 데이터의 개수인데, 미분 시 변하는 것이 아니므로 
은 상수다. Σ 역시 합계를 나타내는 것이며, 둘 다 미분에서는 신경 쓸 필요가 없다. 따라서 미분할 내용은 (Wx + b - y)2이다.
W에 대해 편미분하면 2x2W + 2xb - 0 - 2xy + 0 + 0이다. 그리고 b에 대해 편미분하면 0 + 2xW - 2y - 0 + 2b + 0이다. 이제 편미분할 때 무시했던 과 Σ를 다시 붙이면 다음과 같다.
W 기울기 = 
b 기울기 = 
마지막으로 W와 b를 변경하면서 반복해 계산하는데, 경사하강법 계산에서 비용함수 결과가 0이면 종료하고, 그렇지 않으면 W와 b를 업데이트해 값을 찾아내면 된다. 이러한 과정이 머신 러닝에서 가장 간단한 선형 회귀 알고리즘인 경사하강법이다.
경사하강법에는 학습률이라는 것이 있다. 그림 7-9와 같이 손실함수의 한 점에 접하는 직선을 손실함수의 좌우를 번갈아가면서 긋는다. 이때 적절하게 이동 거리를 주는데, 이런 이동 거리를 학습률이라고 한다.
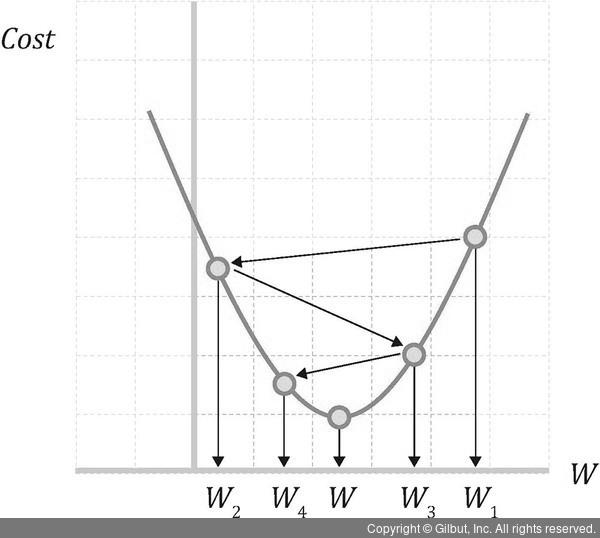
▲ 그림 7-9 경사하강법으로 학습률만큼 이동해 최솟값을 찾아가는 과정