예를 들어, 들판에 메뚜기가 어떻게 늘어나는지 살펴볼까요? 메뚜기가 처음부터 마지막까지 계속해서 증가한다고 볼 수도 있지만, 실제로는 그렇지 않습니다. 메뚜기의 수가 처음에는 서서히 증가하다가 어느 순간 많이 증가하고, 마지막에는 그 증가하는 수가 줄어듭니다.

로지스틱 그래프를 살펴보면 이와 비슷합니다. 처음에는 서서히 증가하다가 어느 순간 그 증가하는 양이 많아지게 됩니다. 그리고 마지막에는 증가하는 양이 서서히 줄어들죠. 이와 같이 어떤 생물들이 어떤 식으로 증가하는지 설명하는 모델이 바로 로지스틱 함수입니다.

그리고 시그모이드 곡선은 로지스틱 곡선의 특수한 사례입니다.

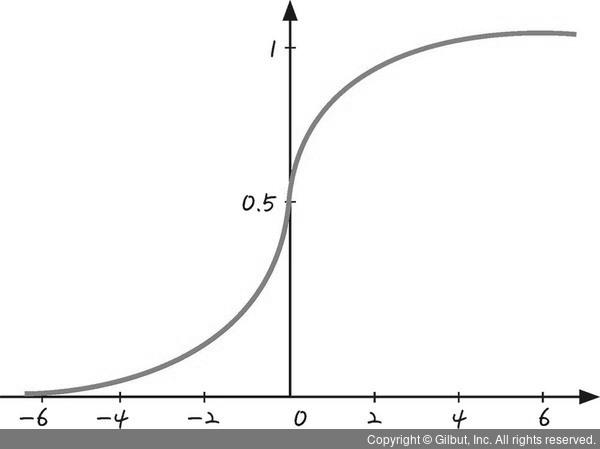
그림 5-10 | 로지스틱 곡선

시그모이드 함수도 로지스틱 함수와 비슷하게 S자 모양을 하고 있습니다. 하지만 입력값에 따른 출력값을 보면 로지스틱 함수와의 차이점이 보입니다. 2, 4, 6 같은 양수를 입력값으로 넣으면 출력값이 1에 가까워지지만, -2, -4, -6, -8 같은 음수를 넣으면 출력값이 0에 가까워지는 것을 볼 수 있습니다.

만약 여러 뉴런에서 들어온 신호 세기를 모아서 그 값이 0보다 클수록 1에 가까운 숫자로 바꿔 줍니다. 반대로 신호 세기가 0보다 작을수록 0에 가까운 숫자로 바꾸어 주는 특징을 가진 활성화 함수가 바로 시그모이드 함수입니다.