이렇게 그래프를 눈으로 볼 때에는 아래로 내려가면 될 것이라고 생각할 수 있지만, 그래프의 형태를 볼 수 없을 때에는 어떻게 해야 할까요? 바로 b에서 a로 점점 이동해야 합니다. 이때 가장 큰 특징이 바로 각 지점에서의 기울기입니다. b 지점의 기울기(이때 기울기는 양수와 음수가 중요한 것이 아니라 그 크기가 중요합니다)가 가장 크며, a 지점으로 갈수록 기울기의 크기가 작아지는 것을 볼 수 있습니다. 그리고 우리가 목표로 하는 a 지점의 기울기는 가장 작은 0입니다.

이처럼 오차가 가장 적은 지점으로 가중치의 값을 이동시키기 위해서는 기울기가 점점 줄어드는 방향으로 이동해야겠죠? 기울기를 보고 기울기가 줄어드는 쪽으로 가중치 값을 이동하는 이 방법의 이름이 바로 경사 하강법(Gradient Descent)입니다.

여러분은 미분에 대해 들어본 적 있나요? 미분을 간단히 말하면 ‘한 지점에서의 기울기’를 의미합니다.

다음과 같은 그래프가 있습니다. A라는 지점과 B라는 지점을 이으면 다음과 같은 기울기가 나오죠? 그런데 이때 A와 B 지점의 간격을 서서히 좁히면 어떻게 될까요? 그리고 A와 B가 만난다면요? 이때의 기울기가 바로 한 지점에서의 기울기가 됩니다.

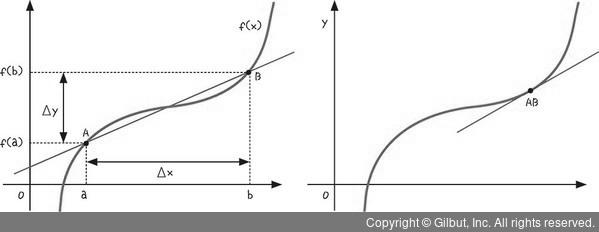
그림 6-5 | 한 지점에서의 기울기: 미분